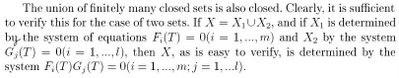Lars Hörmander ou comment présenter l'analyse complexe efficacement...

Il existe de nombreux livres traitant de l'analyse complexe, mais l'un d'eux nommé Introduction to Complex Analysis in Several Variables est présenté par certains comme LA référence. Cet ouvrage, écrit par le lauréat de la médaille Fields Lars Hörmander est en effet très joli, mais est à déconseiller à quiconque veut s'initier à cet belle branche des mathématiques qu'est l'analyse complexe. L'auteur fait preuve d'une concision remarquable, ce qui troublera sans doute les néophytes. Pourtant sa présentation va droit à l'essentiel, les démonstrations sont les plus courtes et les plus agréables qu'on puisse faire il me semble. Ce n'est pas étonnant de la part d'un mathématicien qui a reçu la médaille Fields d'écrire un cours qui soit d'une clarté et d'une efficacité démentes. Par exemple, il prouve dès la page 2 du manuel (!) la formule dite de Cauchy-Pompeiu, après avoir rappelé la formule de Stokes:



S'en suit la démonstration proprement dite:



Comme on le voit, l'auteur boucle la démonstration du théorème en moins de 6 lignes. Il utilise dans celle-ci sans le mentionner le théorème de convergence dominée de Lebesgue. De fait, les prérecquis supposés par l'auteur concernent tous les savoirs de base en analyse fonctionnelle. On peut rajouter aussi qu'il est nécéssaire d'avoir quelques connaissances sur les formes différentielles pour bien comprendre de quoi il retourne, puisqu'il utilise le point de vue des formes différentielles pour traiter de la théorie des fonctions holomorphes (ou analytiques).

En bref, je resumerais tout cela par un seul mot: efficacité.

Qu'est-ce qu'une limite inductive ?

Comment construire un nouvel ensemble qui soit "interessant" à partir d'une collection d'ensembles donnée? Avec par exemple la notion de limite inductive, qui est évoquée de manière extrêmement brève, mais particulièrement concise par Roger Godement (dont les livres sont tous des merveilles-j'espère avoir l'occasion d'en reparler dans d'autres messages) dans le livre intitulé Théorie des faisceaux. Le fait que l'objectif avoué dans la préface de cet ouvrage est d'abord de présenter un

exposé complet, i.e moins incomplet que les autres, de la théorie des faisceaux

explique le fait que l'auteur ne s'étende pas plus que cela sur la notion de limite inductive; pourtant, elle est présentée avec rigueur et précision (comme toujours avec Godement, ancien membre du collectif Bourbaki):



Certes, l'auteur ne revient pas sur la notion d'ensemble ordonné filtrant décroissant, ni sur celle d'ensemble somme et on le comprend car le but du livre est tout autre. Rappelons ce qu'elles sont: la première signifie que l'ensemble I considéré est muni d'une relation d'ordre =< telle que pour tous éléments i et j de I, on peut trouver un élément k dans I tel que k =< i,j. La seconde notion est purement ensembliste, l'ensemble somme des Ei étant l'ensemble des éléments x tels qu'il existe i dans I tel que x appartient à Ei. L'existence d'un tel ensemble (qu'on peut voir comme la réunion de tous les Ei) est assurée par l'axiome dit de la réunion, un des axiomes de bases de la théorie des ensembles de Zermelo-Fraenkel (ZF), théorie dans laquelle on se place usuellement en mathématiques.

Mais à quoi ça sert une limite inductive d'ensemble ? Par exemple à montrer l'existence d'une extension algébriquement close pour tout corps (c'est-à-dire, pour un corps donné, créer un ensemble plus gros le contenant, et qui soit un corps dans lequel tout polynôme a au moins une racine); car ce qui est pratique avec la limite inductive, c'est que si les Ei sont initialement muni d'une structure de groupe (resp. anneau) au départ, on peut alors munir cet ensemble d'une structure de groupe (resp. d'anneaux), ce que mentionne quelques lignes plus loin notre ami Roger Godement.

Un peu de géométrie algébrique en apéritif

Dans l'excellent Basic Algebraic Geometry, Igor Shafarevic, spécialiste de géométrie algébrique commence par exposer de manière simple les rudiments de cette matière dans des cas simples, en l'occurence les ensembles algébriques d'un espace affine. Après avoir introduit de très belle manière les courbes algébriques planes (cet auteur, et c'est une chose qu'on retrouve dans plusieurs de ses livres, n'est pas avare en exemple!), notre cher Igor en vient au paragraphe 2 du premier chapitre (lui-même sobrement appelé Fundamental Concepts) à nous parler de ce qu'il nomme les sous-ensembles fermés des espaces affines. Le terme de fermé rappelle des notions topologiques, et c'est de bon augur puisque c'est de cela qu'il s'agit. Au milieu de la page 14, on peut lire:




k désignant un corps algébriquement clos, et A^n l'espace affine de dimension n sur k (qui est unique à isomorphisme d'espace affine sur k près). Ce qu'il désgine par closed subset s'appelle parfois ensemble algébrique. Dans la suite, il va démontrer (sans le dire!) que cet ensemble qu'il vient de se donner (l'ensemble des closed subsets) forme une topologie sur l'ensemble A^n. Il s'agit en fait de la topologie dite de Zariski, découverte par le mathématicien du même nom. Il commence par montrer que l'intersection d'un nombre quelconque d'ensembles algébriques est encore algébrique:





Ce qu'il "omet" de dire (c'est surement une chose évidente pour un mathématicien de son calibre) c'est que l'idéal A "gothique) est engendré par un nombre fini d'éléments G1,...,Gm car l'anneau des polynômes à plusieurs variables à coefficients dans k est noetherien. Ensuite, il passe à la démonstration du deuxième axiôme d'une topologie: l'union d'un nombre fini de fermés est fermé.









Cette topologie qu'il vient de construire joue un rôle important dans l'étude des courbes algébriques, et se généralise même a des espaces plus généraux et compliqués que l'espace affine A^n considéré ici.